L'EQUAZIONE DI SCHRÖDINGER

Poco tempo dopo l'ipotesi di Louis de Broglie sulle proprieta' ondulatorie della materia, il matematico e fisico austriaco Erwin Schrödinger, basandosi proprio sulla natura ondulatoria dell'elettrone, formulo' una teoria, nota con il nome di Meccanica Ondulatoria, con la quale era possibile descrivere matematicamente le proprieta' ondulatorie di particelle microscopiche come l'elettrone.

Schrödinger ottenne un'equazione valida per particelle vincolate (cioe' soggette a forze) cosi' come si presentavano gli elettroni in un atomo, legati al nucleo dalla forza elettrica di attrazione. La sua equazione ammetteva soluzioni solo nel caso in cui l'energia delle particelle assumeva dei valori ben definiti, contrariamente a quanto succedeva per una particella libera di muoversi, la quale poteva assumere un qualsiasi valore di energia.

La teoria di Schrödinger confermava ulteriormente il concetto di “quantizzazione dell'energia degli elettroni atomici” previsto da Bohr.

Il modello di Bohr presentava pero' delle limitazioni. Infatti, esso non giustificava il motivo per cui alcune righe spettrali risultassero piu' luminose di altre e non permetteva di calcolare la probabilita' di transizione tra i livelli energetici atomici. Inoltre, gli elettroni venivano considerati come dei piccoli pianeti in rotazione intorno al nucleo, con raggio dell'orbita ed impulso ben definiti; cio' violava il principio di indeterminazione di Heisenberg secondo il quale la posizione e l'impulso di una particella non potevano essere determinati contemporaneamente in maniera esatta.

Schrödinger introdusse il concetto di funzione d'onda Ψ di una particella, il quale, sostituendo l'idea di “traiettoria precisa” per una particella, divenne il principale concetto della Teoria Quantistica. La funzione d'onda consisteva in una funzione matematica contenente tutte le informazioni riguardanti l'evoluzione nello spazio e nel tempo di un'onda-particella quantistica entro un campo di forza conservativo. Il nome “funzione d'onda” derivo' dal fatto che una tale funzione era in grado di descrive il comportamento di un corpuscolo materiale considerato come un'onda.

L'equazione di Schrödinger indipendente dal tempo

Schrödinger, trattando matematicamente le onde di de Broglie, giunse ad una equazione differenziale.

L'equazione di Schrödinger unidimensionale ed indipendente dal tempo, per coordinate cartesiane, e' la seguente:

(-ћ²/2m)d²Ψ(x)/dx² + U(x)Ψ(x) = EΨ(x)

con ћ=h/2π → ћ=1,055∙10^-34 J∙s

Se si considerano le tre dimensioni (x,y,z), l'equazione assume la forma:

(-ћ²/2m)(δ²Ψ/δx²+δ²Ψ/δy²+δ²Ψ/δz²) + U(x,y,z)Ψ(x,y,z) = EΨ(x,y,z)

In quest'ultima espressione si nota come dalla semplice derivata presente nell'equazione unidimensionale si sia passati alle derivate parziali, fatte rispettivamente rispetto alle coordinate cartesiane x,y,z.

L'equazione di Schrödinger indipendente dal tempo puo' anche essere scritta in una forma piu' sintetica:

[(-ћ²/2m)∇² + U(x,y,z)]∙Ψ(x,y,z) = E∙Ψ(x,y,z)

dove si e' introdotto l'operatore di Laplace ∇²=∂²/∂x²+∂²/∂y²+∂²/∂z², che indica l'operazione matematica da compiere sulla funzione d'onda ψ(x,y,z).

L'equazione di Schrödinger indipendente dal tempo fissa la dipendenza spaziale della funzione d'onda associata ad ogni particella che si muove in un campo di forza conservativo. Tale funzione d'onda contiene tutte le informazioni fisiche (misurabili) sulla particella.

L'equazione di Schrödinger dipendente dal tempo

Questa equazione puo' essere ricavata partendo dal principio di conservazione dell'energia che, per una particella di quantita' di moto p e di energia potenziale U costante (indipendente dal tempo), e' esprimibile nella forma:

E = p²/2m + U(x,y,z)

Alle grandezze classiche p ed E devono essere sostituiti i seguenti operatori quantistici, che devono operare sulla funzione d'onda Ψ(x,y,z,t):

p → (h/j2π)∙∇

E → -(h/j2π)∙∂/∂t

dove: ∇ e' l'operatore gradiente; ∂/∂t e' la derivata parziale fatta rispetto al tempo; h e' la costante di Planck; j e' l'unita' immaginaria (j = √-1).

L'espressione finale dell'equazione di Schrödinger dipendente dal tempo e':

-(h/j2π)∙∂Ψ(x,y,z,t)/∂t = (h²/j²4π²2m)∙∇²Ψ(x,y,z,t) + U(x;y;z)∙Ψ(x,y,z,t)

Introducendo il termine ћ = h/2π, l'equazione diventa:

jћ∂Ψ(x,y,z,t)/∂t = -(ћ²/2m)∙∇²Ψ(x,y,z,t) + U(x;y;z)∙Ψ(x,y,z,t)

L'equazione di Schrödinger dipendente dal tempo fissa l'evoluzione temporale della funzione d'onda associata ad ogni particella che si muove in un campo di forza conservativo. Tale funzione d'onda contiene tutte le informazioni fisiche (misurabili) sulla particella.

Lo spettro dell'atomo di idrogeno e' perfettamente descrivibile con l'equazione di Schrödinger.

Infatti, si puo' dimostrare come, in questo caso particolare, le soluzioni di tale equazione, che conviene esprimere utilizzando le coordinate polari sferiche (r, θ, φ) per via della simmetria sferica dell'atomo, conducano a 3 numeri quantici: n, l ed m_l, associabili allo stato dell'elettrone nell'atomo.

Osservazione:

L'equazione di Schrödinger dipendente dal tempo, in una dimensione spaziale, assume la forma:

-(ћ²/2m)δ²Ψ(x,t)/δx² + U(x)Ψ(x,t) = jћ∂Ψ(x,t)/∂t

Nel caso particolare di una particella libera, per la quale U(x)=0, la funzione d'onda, soluzione dell'equazione di Schrödinger, e' praticamente un'onda piana contenente la relazione di de Broglie per l'impulso e la relazione di Planck per l'energia:

Ψ(x,t) = Ae^i(kx-ωt)

con k=2π/λ=2πp/h (numero d'onda) e ω=2π/T=2πʋ=2πE/h (pulsazione)

Per una particella libera (senza vincoli di potenziale) l'equazione di Schrödinger fornisce soluzioni secondo le quali la particella puo' assumere tutti i valori di energia. Quindi, l'energia di una particella libera non e' quantizzata.

Significato della funzione d'onda

Fu il fisico tedesco Max Born a dare un'interpretazione fisica alla funzione d'onda Ψ(x,y,z,t). Egli suggeri' che la probabilita' di trovare una particella in una data regione dello spazio risultava proporzionale al valore di ψ².

La giustificazione di tale interpretazione e' da attribuire al fatto che una particella quantistica non ha solo natura corpuscolare, ma possiede anche una natura ondulatoria.

In definitiva, non e' possibile parlare di posizione precisa di una particella nello spazio, ma ha senso parlare solo di probabilita' di trovare la particella, durante l'intervallo di tempo Δt (centrato nell'istante t), in una regione di volume ΔV (centrato nel punto di coordinate (x,y,z)). Questa probabilita' e' data dall'espressione:

P = |ψ(x,y,z,t)|²ΔVΔt

ψ² individua percio' una densita' di probabilita' intesa come rapporto tra la probabilita' di trovare la particella entro una piccola regione dello spazio ed il volume di tale regione.

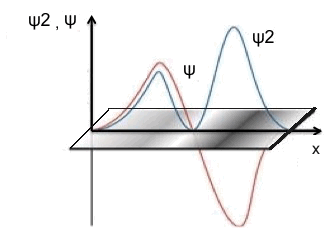
La figura che segue fornisce l'interpretazione di Born della funzione d'onda:

La funzione d'onda e' indicata con Ψ (curva arancione). La densita' di probabilita' (curva blu) e' data dal quadrato della funzione d'onda ed e' rappresentata dalla densita' dell'ombreggiatura nella banda sottostante.

Secondo l'interpretazione di Born, in tutte le zone in cui ψ² e' grande la particella presenta elevata densita' di probabilita', mentre dove ψ² e' piccola la particella possiede bassa densita' di probabilita'. Quindi, nelle zone in cui ψ si annulla risulta nulla anche ψ² e si ha densita' di probabilita' pari a zero per la particella. Il punto in cui ψ passa per lo zero si definisce nodo della funzione d'onda. Pertanto, si puo' affermare che:

in corrispondenza di un nodo della funzione d'onda la particella ha densita' di probabilita' nulla.

E' importante sottolineare che, mentre nella Meccanica Classica lo stato di una particella viene definito attraverso il valore esatto di due quantita' osservabili: posizione e quantita' di moto, in Meccanica Quantistica lo stato di una particella, come l'elettrone, e' descritto dalla sua funzione d'onda Ψ, soluzione dell'equazione di Schrödinger.

Congresso Solvay

L'introduzione della funzione d'onda Ψ e del suo modulo al quadrato provoco' una serie di discussioni. Il culmine si ebbe al Congresso Solvay del 1927, durante il quale si scontrarono due fazioni:

• il gruppo formato da Born, Heisenberg, Dirac e Pauli, con a capo Bohr. Questo gruppo si rivelo' vincente ed i suoi esponenti furono considerati successivamente membri della Scuola di Copenaghen;

• il gruppo formato da Planck, Einstein, Schrödinger e de Broglie. Questo fu il gruppo sconfitto.

Secondo la tesi portata avanti dai seguaci di Bohr, la Teoria Quantistica diventava una teoria completa e definitiva.

Modello atomico della Meccanica Ondulatoria

L'equazione di Schrödinger, una delle piu' importanti equazioni della Meccanica Quantistica, ha permesso di ottenere una conoscenza dell'atomo molto piu' approfondita e completa. Con essa si e' potuto elaborare un nuovo modello atomico, quello della Meccanica Ondulatoria, successivo al modello di Bohr. Con il modello atomico della Meccanica Ondulatoria, attraverso la funzione d'onda, si e' giunti a definire lo stato energetico degli elettroni in accordo con gli stati energetici indicati da Bohr. Inoltre, l'idea di Born di funzione d'onda, intesa come onda di probabilita', ha portato al concetto di orbitale, definibile come quella zona attorno al nucleo in cui la probabilita' di trovare l'elettrone risulta molto alta. Questo concetto, piu' avanzato e sottile rispetto a quello delle orbite di Bohr, ha permesso infine di costruire l'efficace “modello atomico ad orbitali”.

CONCLUSIONI

Mentre gli oggetti di grandi dimensioni seguono le leggi della Meccanica Classica (leggi di Newton), il comportamento di piccole particelle, come elettroni, atomi e molecole e' descritto molto meglio dalla Meccanica Quantistica, basata sulle proprieta' ondulatorie della materia. La quantizzazione dell'energia e' proprio una conseguenza di tali proprieta'.

La Meccanica Quantistica e' in grado di spiegare tutti i fenomeni fino ad ora osservati su scala atomica. In particolare, essa permette di:

• descrivere correttamente il moto di particelle soggette a campi di forza;

• determinare i livelli energetici dell'atomo di idrogeno e le corrispondenti funzioni d'onda dell'elettrone (orbitali);

• ottenere, applicando il principio di esclusione di Pauli, la configurazione elettronica degli atomi piu' complessi;

• ottenere la probabilita' di transizione tra due diversi livelli energetici di un atomo, integrandola con la teoria quantistica della radiazione elettromagnetica.

Fino ad ora la Meccanica Quantistica non e' stata contraddetta da alcun fatto sperimentale.